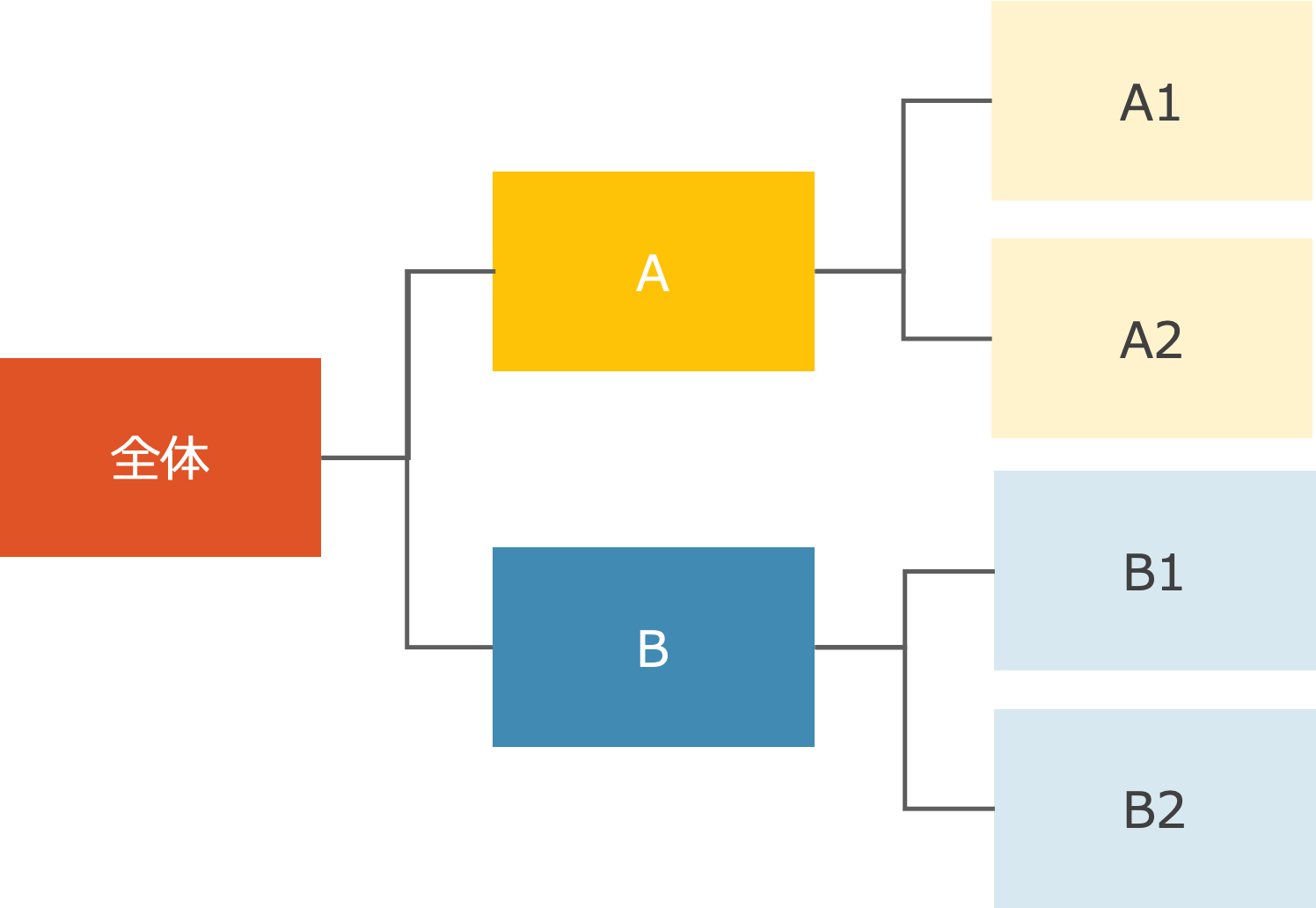
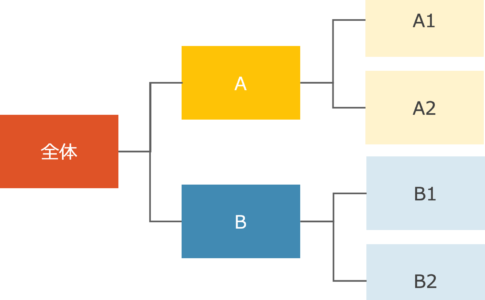
ロジックツリーとは、分析手法の1種でもれなくダブりなく(MECE)を意識して上位概念を下位の概念に枝分かれさせて分解していく方法のことです。
全体をいくつかの中項目分け、さらに小項目に分けるといった多段階構造が、木の幹のように枝分かれしていくように見えることからロジックツリーと名付けられました。
どういう場面に役立つかというと
- 問題解決をするときに問題の1番大きなポイントはどこにあるのかのWhereを絞り込む
- その問題が発生している原因のWhyを解明
- どのような解決策のHowがあるか
といった、幅広く考えるために用いられます。
ロジックツリーを使うと、体系的にアプローチすることで思考のスピードをアップさせることができるだけでなく、全体像を見る意識付けができ思考の幅を広げて、見落としを減らすことができるなどのメリットがあります。
よく用いられる分解の方法を2つご紹介します。
層別分解
層別分解とは、全体を複数の部分に切り分けていきます。
例えば、ある企業で急激に増えている離職率の対策を打ちたいと考えているとします。
そこで層別分解を使って、離職者の傾向を探っていきます。
社員全体を、年代や所属部署、残業時間などで分けていきます。
こうすればどの年代に離職者が多いのか、所属する部署の違いはあるのか、残業時間は影響しているのか、といった離職者の傾向を掴みやすくなり、対策を考えやすくなります。
変数分解
変数分解とは、かけ算を利用して分解します。
例えば売上高は数量×単価に、さらに単価は1×−割引率のように分配することができます。
こうすることで売上高を伸ばしたいと言う課題があるときに数量を増やすのか、単価を上げるのかあるいは割引率を減らすのかなどと細分化して解決策を検討することが可能となります。
課題解決にロジックツリーを使う癖付けできれば、思考のスピードをアップさせ効率よく仕事に取り組むことができるだけでなく、仕事に質も高まります。